The Math Behind Threat — Half 1

The Math Behind Threat — Half 1

Does the assault actually have a bonus within the sport of world conquest?

A superb buddy of mine (Hey, Aron) not too long ago requested me what the possibilities are for the assault and protection within the board sport Threat. I do know that the conquests of Alexander the Nice and Genghis Khan can’t be absolutely defined by the mechanics of Threat, nevertheless it nonetheless appeared like an intriguing query, and it offers a wonderful illustration of the capability of likelihood and information visualization to tell and energy clever choice making.

For many who don’t know, Threat is a board sport of world conquest the place the attacker rolls (as much as) three cube and the defender rolls (as much as) two cube. The participant whose highest roll is decrease loses a soldier, and a tie goes to the defender. We are going to check with this as the primary battle. If each gamers are rolling not less than two cube, then the participant whose second highest roll is decrease will even lose a soldier. As soon as once more, a tie goes to the defender. We are going to name this the second battle.

After all, it’s clearly a bonus to throw 3 cube as an alternative of two, and the favorability of profitable within the case of a tie is equally apparent. What’s much less apparent is how these benefits stack up in opposition to every different.

(Right here you can discover code wherein I verify the beneath chances.)

Earlier than analyzing the relative chances of protection and assault, let’s first analyze every of them in isolation.

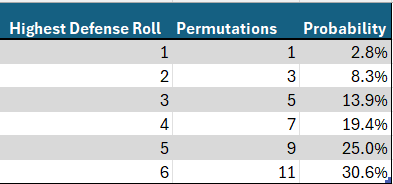
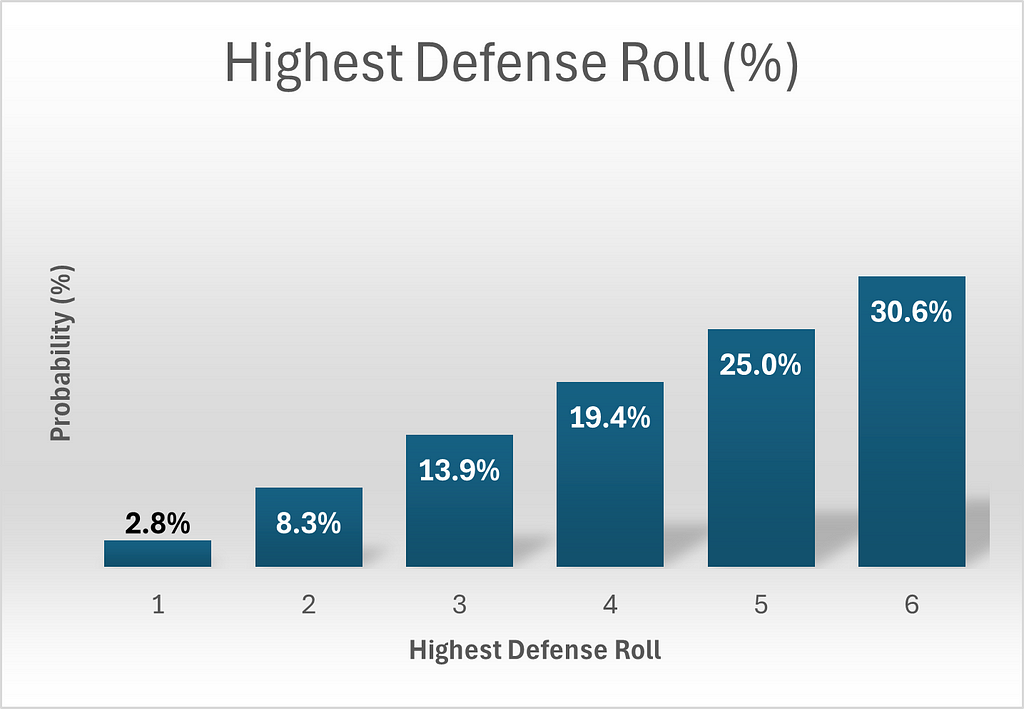
The defender’s flip is easier as he rolls solely two cube, so let’s begin there. There are 11 permutations yielding a highest roll of 6. This may be calculated by contemplating all the chances: {(1,6), (2,6), (3,6), (4,6), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}. By comparable logic, the variety of permutations giving highest rolls of 5, 4, 3, 2 or 1 may be calculated as 9, 7, 5, 3 and 1 respectively. Since there are a complete of 6 x 6 = 36 complete permutations for two cube, we’d like solely divide every permutation rely by 36 to acquire chances. The beneath graphics needs to be useful. Please be aware that in all of the graphics, pink denotes assault and blue denotes protection, consistent with the colour scheme of Threat itself.

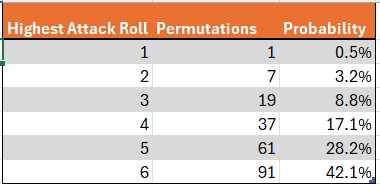
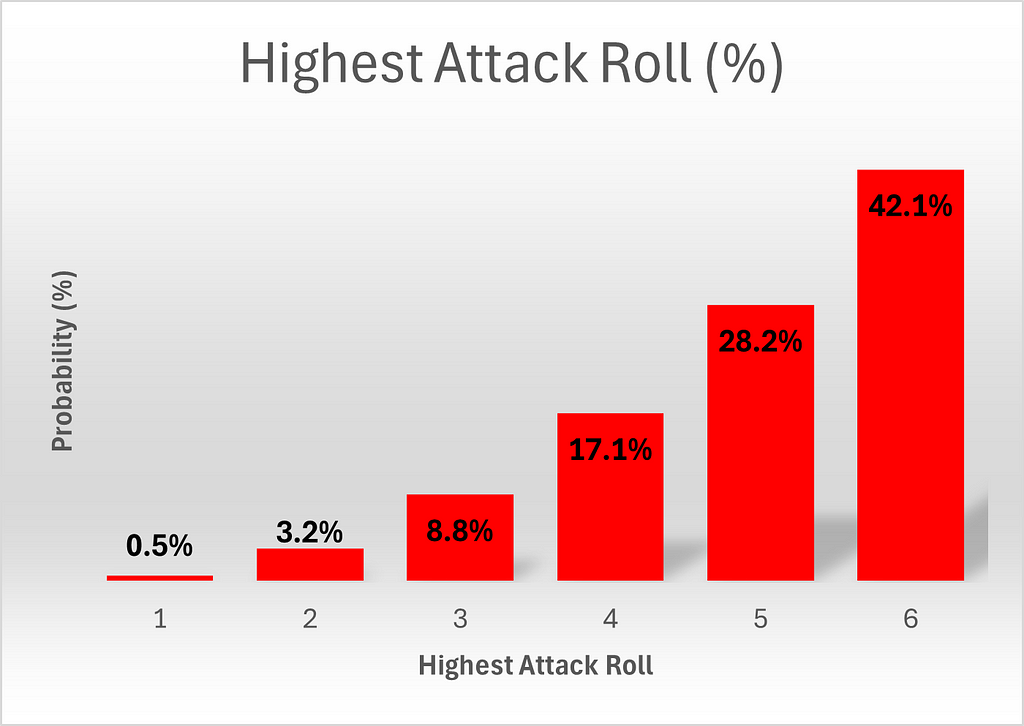
The best roll of the attacker is barely extra complicated, as he rolls 3 cube. To calculate what number of permutations yield a highest roll of 6, let’s begin by fixing the very best roll at 6 and let’s additional stipulate that it happens at die 1. It’s then clear that cube two and three may be something as much as 6, for a complete of 6*6 = 36 outcomes. If we subsequent repair the very best consequence of 6 at die 2, we should restrict the primary die to not being six, since we already thought-about that chance. The third die may be something, for a complete of 6×5=30 extra outcomes. Lastly, we will repair the very best consequence of 6 on the third die, and we all know that we should restrict the primary two cube to not being six, since these prospects have already been counted. This yields an extra 25 outcomes, for a complete of 36+30+25 = 91 of prospects.

We are able to generalize this to calculate the variety of outcomes yielding a highest roll of x. If the very best roll happens at die 1, the second and third die can take any consequence as much as and together with x, for a complete of x² outcomes. If, alternatively, the very best roll happens at die 2, die 1 can take any worth as much as x-1, (since we now have already thought-about the case the place the primary die takes a price of x) and the third die can take any worth as much as x, for a complete of x(x-1)=x²-x extra outcomes. Lastly, we contemplate the choice of die three taking the worth x. Then the one choices not but counted are for the primary and second cube to every take a price as much as x-1, including (x-1)*(x-1) = x²–2x+1 outcomes. Including the whole lot up, we acquire a complete of 3x²–3x+1 ways¹ to acquire a highest roll of x.

Word that the whole variety of permutations is 216, as anticipated, since 6³ = 216, which supplies confidence that these calculations are right.

Subsequent, let’s immediately evaluate the possibilities for assault and protection.

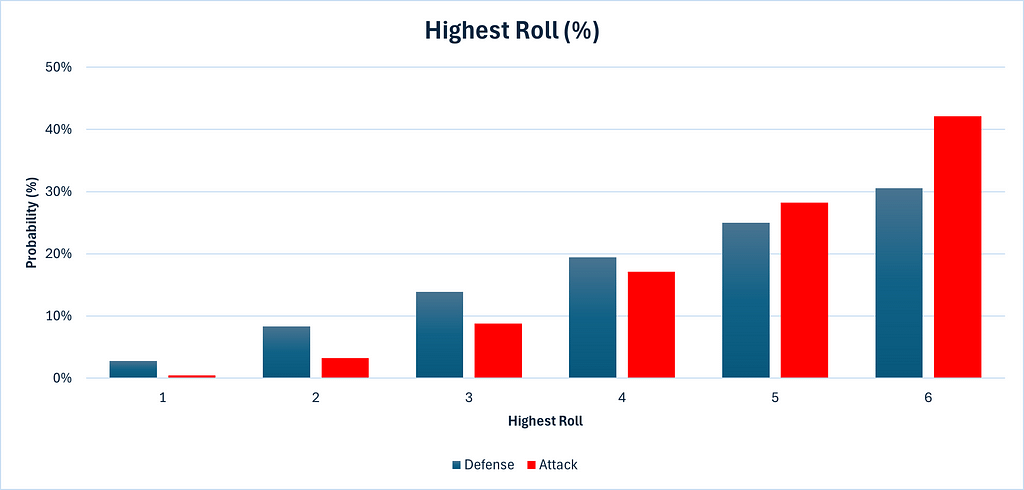
We are able to see that the protection has a better likelihood of getting 1, 2, 3 and 4 as a highest roll than assault does, whereas assault has a better likelihood of getting 5 or 6 as the very best roll than his opponent. That is the third die working within the assault’s favor.

Sufficient stalling, let’s get to the battle.

We should contemplate the 2 battles individually. In Half 1, we’ll analyze the primary battle, of who will win the very best roll, and we’ll go away the evaluation of the second battle, for the 2nd highest roll, for Half 2.

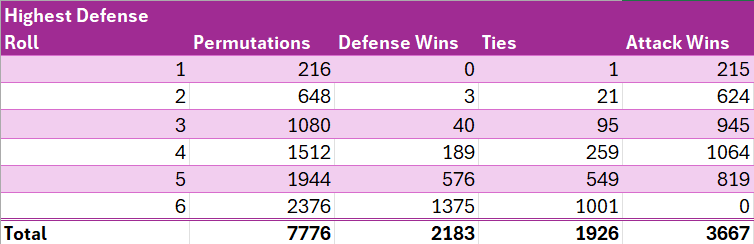
To calculate the likelihood of the attacker profitable the very best roll, we’ll first rely the permutations wherein the defender achieves a highest roll of x and calculate what number of of these permutations would lead to an outright win for the protection, a tie, which fits to the protection, or a win for the assault.

For instance, since, as calculated above, there’s a 9/36 likelihood of the protection’s highest roll being 5, and there are a complete of 6⁵ = 7776 permutations, clearly (9/36) * 7776 = 1944 of these permutations will yield a highest protection roll of 5. To win, the assault then must get a highest roll of 6, the likelihood of which is 91/216, as calculated above, so (91/216) * 1944 = 819 of the 1944 permutations which yielded a highest protection roll of 6 will lead to a victory for assault. To realize a tie, assault should roll a highest roll of 5, the likelihood of which is 61/216, so (61/216) * 1944 = 549 of these permutations will lead to ties, and the rest (1944–819–549 = 576) will lead to outright protection wins.

We are able to make comparable calculations for all attainable outcomes for protection. See the beneath desk.

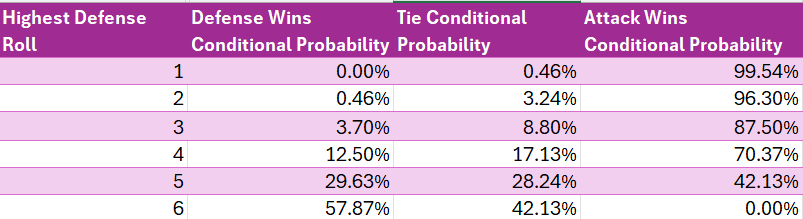
We are able to then calculate the conditional² likelihood of a protection victory, of a tie, and of an assault victory, by dividing the variety of permutations yielding the chosen consequence (e.g. assault wins) by the rely of the broader group of outcomes (e.g. protection rolls a highest roll of 5).

We are able to additionally visualize the conditional chances.

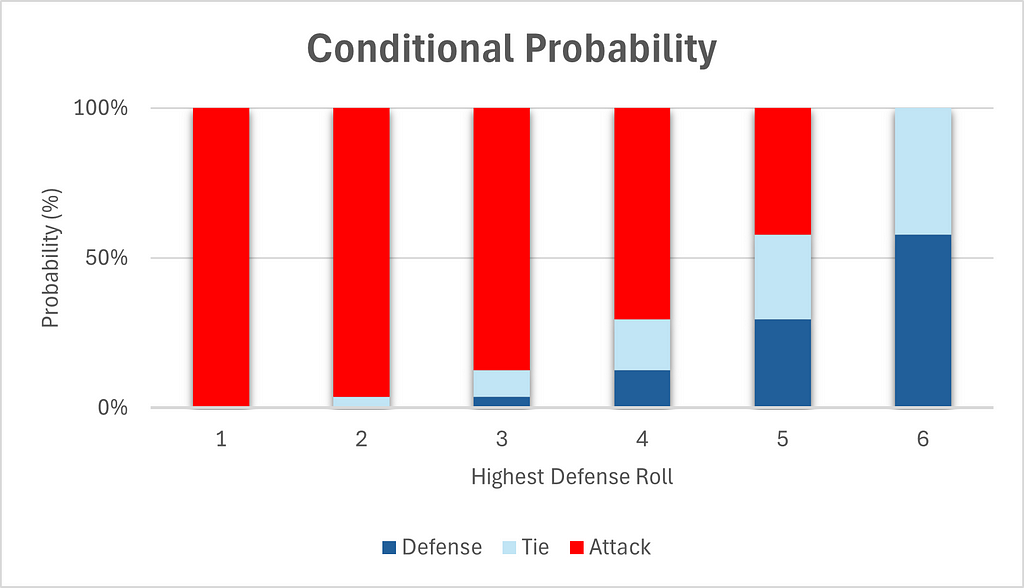
Chart 4 offers the identical misunderstanding that most individuals have initially, specifically that assault has a giant benefit total. However it is because it ignores the possibilities of the very best protection rolls themselves. In truth, larger rolls are considerably extra probably than decrease rolls, as may be seen in Desk 3.

For that reason, complete chances are a simpler measure. It’s even less complicated to calculate the whole likelihood of every consequence. We merely divide every permutation rely by the whole variety of attainable permutations, which is 7776.

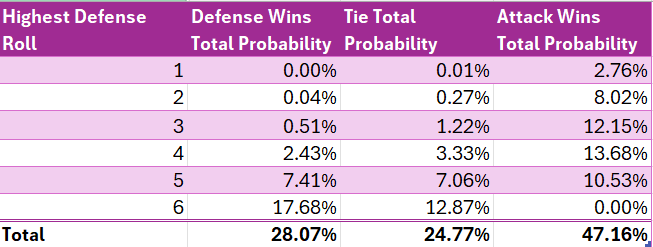
We are able to then sum the whole permutations which lead to a victory for the assault (3667) and divide by the whole attainable permutations (7776) to acquire a win likelihood of 47.15% for the assault.

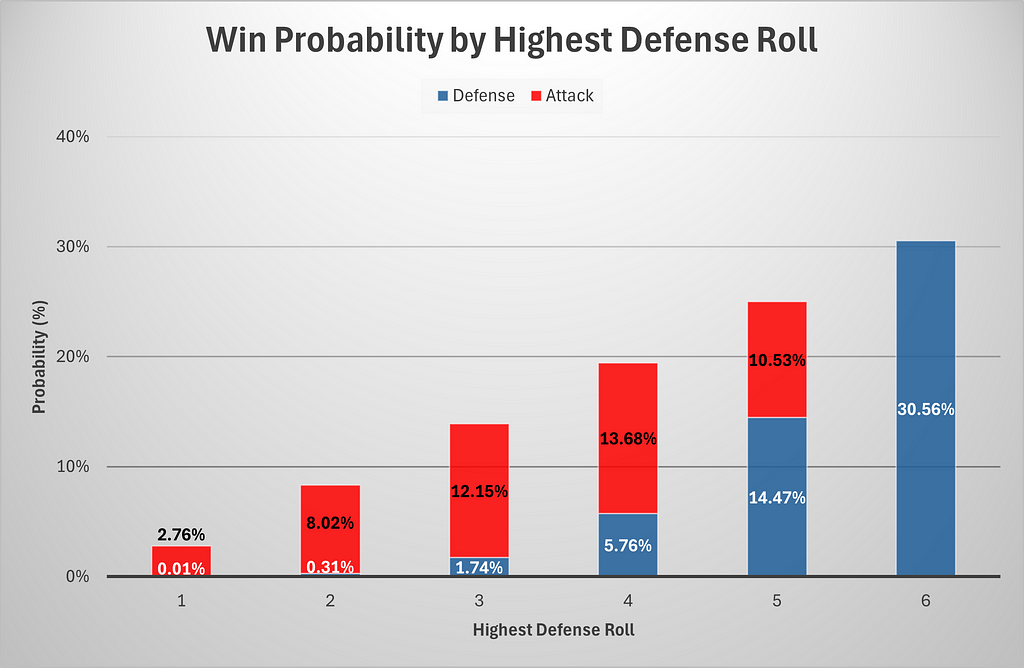
Beneath is a chart of complete win chances by highest defensive roll. We embody a tie as a part of a protection victory for simplicity.

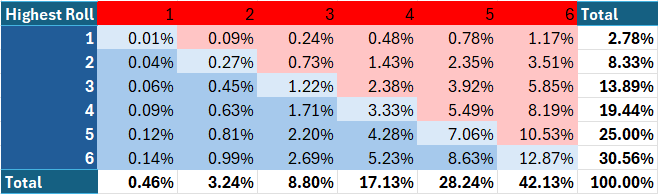
Lastly, we’ll calculate the joint³ chances of every attainable highest roll for each protection and assault. For the reason that highest roll for assault and protection are impartial, we will merely multiply the possibilities collectively to acquire the joint likelihood. Word that within the beneath two graphics, pink point out victory for the assault, whereas blue denotes a defensive victory and pale blue signifies a tie, which fits to the protection.

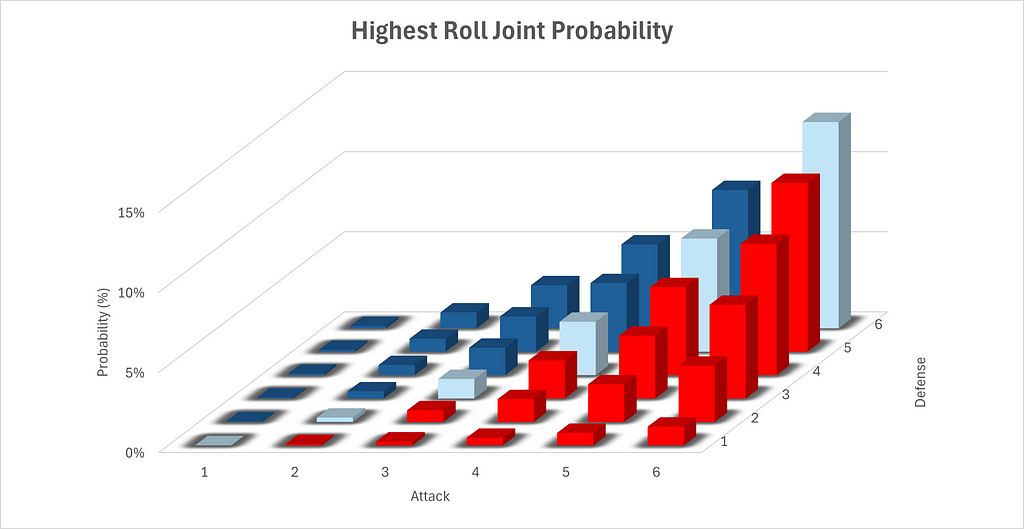
We are able to additionally graph this information visually. Please be aware the configurations of the axes within the beneath chart, which have been configured to permit for maximal visibility.

Conclusions

1. The likelihood of a victory for the assault is 47.15%. This may be seen clearly in Desk 5. We undergo the formal math within the footnotes⁴.
2. The likelihood of an outright victory for the protection is 28.07%. This may be seen clearly in Desk 5.
3. The likelihood of a tie, which fits to the protection after all, is 24.77%. This may be seen clearly in Desk 5.
4. If the protection’s highest roll is 4, he/she has solely a 29.63% likelihood of profitable. This may be calculated by summing the protection win chances on row 4 of Desk 6 and dividing by the row complete.
5. To ensure that the protection to have a better likelihood of profitable outright than assault, he must get a highest roll of 6. This may be seen on rows 5 and 6 of Desk 3 and Desk 4.
6. The probably total consequence, at 12.87% is for each assault and protection to roll highest rolls of 6, giving protection the victory. This may be seen clearly in Desk 6.
7. Of the instances wherein the assault wins, essentially the most generally occurring means for this to occur is for the protection to roll a highest roll of 4. This case constitutes 29.02% of assault’s victories. This may be calculated by observing the assault proportion for a protection roll of 4 in Desk 5 and dividing by the column complete.
8. Solely 5.86% of assault’s victories are available instances the place the protection’s highest roll is 1. The refined, nearly paradoxical level right here is that if protection’s highest roll was 1, you may be nearly positive (99.54%) that assault wins, but when assault wins, you may nonetheless be assured (94.14%) that protection did not roll a highest roll of 1, though admittedly, not as assured as you had been (97.2%) earlier than you discovered that assault gained. (Likelihood is superior.) The primary quantity may be calculated from Desk 5. The second quantity is taken immediately from Desk 4. The third is the complement of the primary, and the fourth may be calculated from Desk 1.

So the assault is definitely at an obstacle for the primary battle. So how was Genghis Khan in a position to rout his enemies so successfully in warfare? Maybe this factors to better subtleties awaiting us within the matter of the second battle. Or possibly this demonstrates a breakdown within the potential of Threat to elucidate historical past’s best conquests. Or maybe, much more tantalizingly, each?

See you in Half 2.

1. For the mathematically inclined, this appears to point that the sum of 3x²-3x+1 for all x as much as and together with okay is the same as k³, to fulfill the plain requirement that summing the permutations yielding a highest worth of x, for all x as much as okay, should equal the whole variety of permutations accessible with 3 cube yielding okay alternate options. And certainly, a easy proof by induction yields this consequence. Clearly this holds for the bottom case of 1, since 3(1)²-3(1)+1 = ¹³. Then we should show that the sum of 3x²-3x+1 for all x as much as and together with okay is the same as k³, utilizing the idea that the sum of 3x²-3x+1 for all x as much as and together with k-1 is the same as (k-1)³. Since (k-1)³ = k³-3k²+3k-1, clearly including 3k²-3k+1 will equal k³. QED.
2. Conditional likelihood means the likelihood given some situation. For instance, if the protection rolls a highest roll of 6, then the assault has a conditional likelihood of victory of 0%, since he can not win in that case. However that’s solely if the protection rolls a highest roll of 6.
3. Joint likelihood merely means the likelihood of two occasions co-occurring.
4. To formalize the maths, we’d like some notation. Let A₁ and D₁ check with the very best cube rolls of the assault and protection, respectively. Moreover, let d point out attainable highest rolls of protection, which clearly can take any worth between one and 6. Then the likelihood of a win for assault may be calculated by calculating the beneath summation:

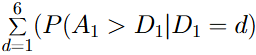
The Math Behind Threat — Half 1 was initially revealed in In the direction of Information Science on Medium, the place individuals are persevering with the dialog by highlighting and responding to this story.

Supply hyperlink